Fast Dynamic Time Warping

This example shows how to compute and visualize the optimal path when computing the Fast Dynamic Time Warping distance between two time series. It is implemented as pyts.utils.fast_dtw().

import numpy as np
import matplotlib.pyplot as plt
from pyts.utils import fast_dtw

# Parameters
n_samples, n_features = 2, 48

# Toy dataset
rng = np.random.RandomState(41)
x, y = rng.randn(n_samples, n_features)

# Dynamic Time Warping
region, D, path = fast_dtw(x, y, dist='absolute', window_size=6,
                           approximation=False, return_path=True)

# Visualize the result
timestamps = np.arange(n_features + 1)
matrix = np.zeros([n_features + 1, n_features + 1])
for i in range(n_features):
    for j in region[i]:
        matrix[j, i] = 0.5
for i in range(len(path)):
    matrix[path[i][0], path[i][1]] = 1

plt.figure(figsize=(8, 8))
plt.pcolor(timestamps, timestamps, matrix, edgecolors='k', cmap='Greys')
plt.xlabel('x', fontsize=20)
plt.ylabel('y', fontsize=20)
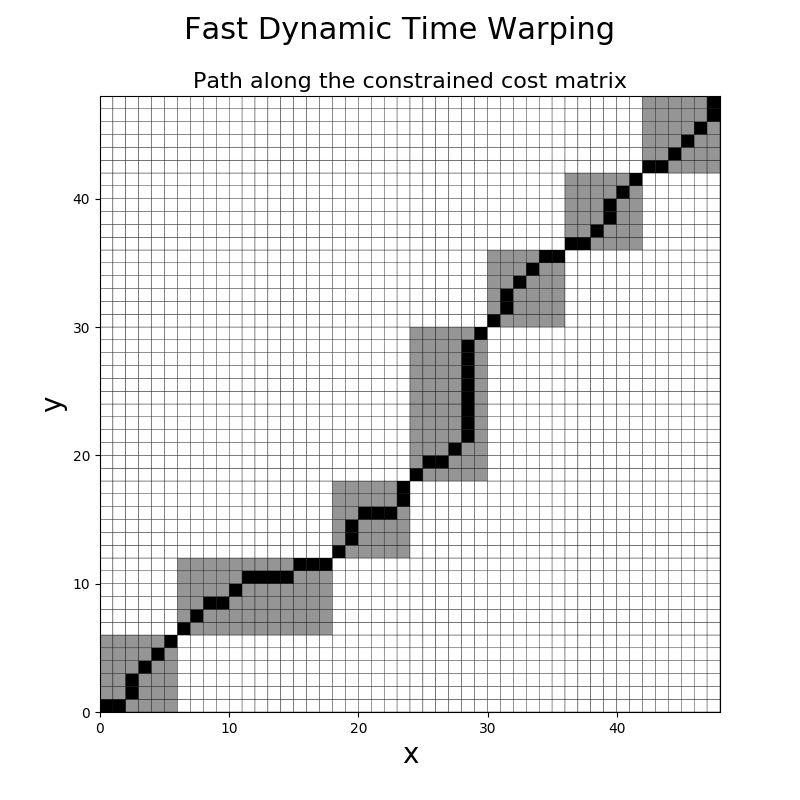
plt.title("Path along the constrained cost matrix", fontsize=16)
plt.suptitle("Fast Dynamic Time Warping", fontsize=22)
plt.show()

Total running time of the script: ( 0 minutes 0.137 seconds)